Table of contents
- Входные данные
- Основные этапы алгоритма
- Точка пересечения отрезка и плоскости
- Определение относительного положения узлов сетки
- Пересечение ребер плоскостью
- Перестроение сетки в месте пересечения
- Выделение двумерных полигонов в месте рассечения
- Триангуляция двумерных полигонов
- Вставка триангуляции полигона в трехмерную сетку
- Заключение
- Ссылки
В статье рассмотрен один из подходов к разбиению триангуляционной сетки плоскостью. Это не какой-то новый подход к разбиению, а лишь вариант алгоритма, построенный на базе уже существующих.
Входные данные
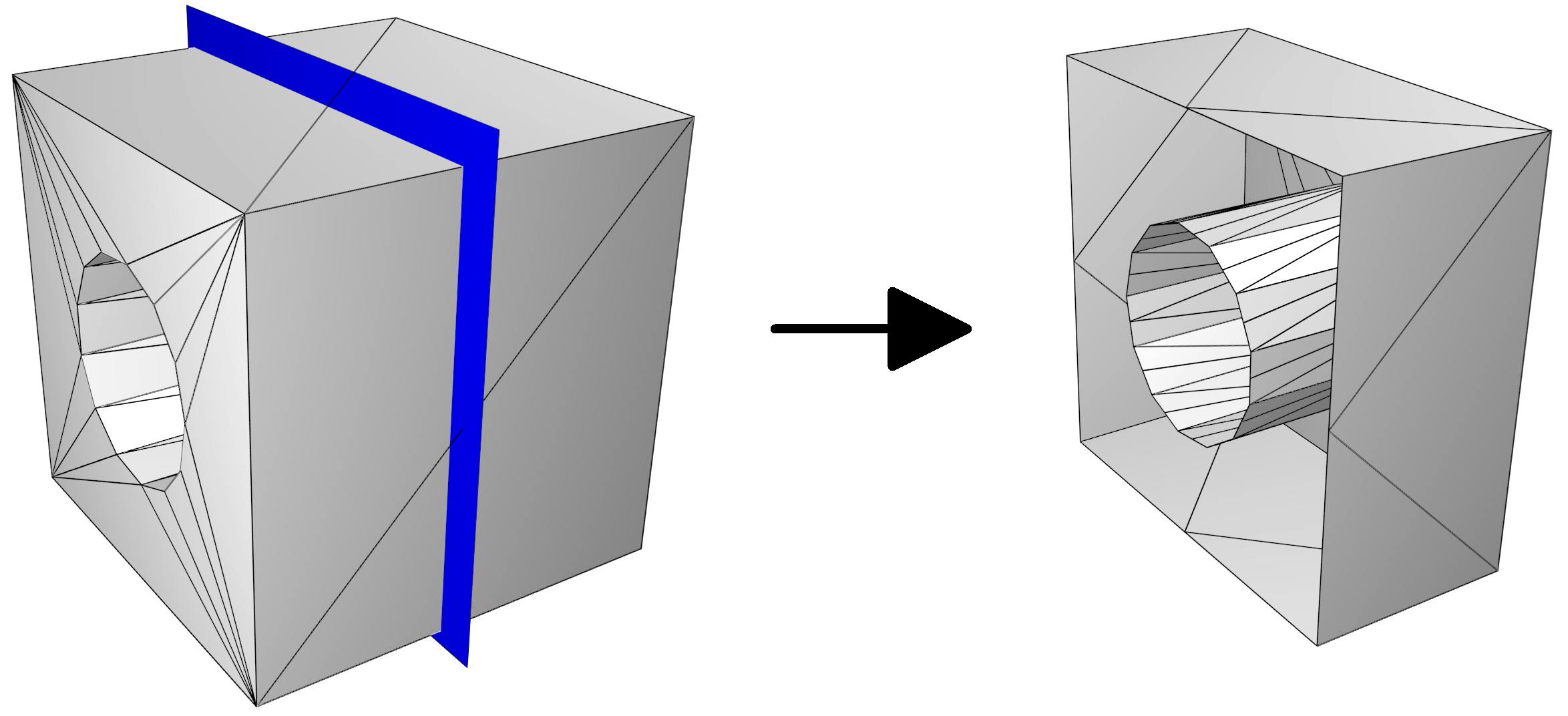
Рассмотрим триангуляционную сетку M некоторой геометрической модели и плоскость S (выделена синим) в трехмерном пространстве. Допускаем, что сетка M не имеет самопересечений.

Выбор структуры данных для представления сетки триангуляции зависит от поставленных задач. Мы применим структуру «Узлы, ребра и треугольники» [1, с17]. В силу своей полноты она несколько упрощает реализацию алгоритма разбиения плоскостью, но в то же время усложняет собственную поддержку. С другими типами структур можно ознакомиться здесь [1, с12].
Основные этапы алгоритма
На схеме ниже показаны основные этапы алгоритма разбиения сетки плоскостью. Основная идея заключается в рассечении исходной сетки плоскостью с последующим заполнением образовавшихся пустот новой триангуляцией.
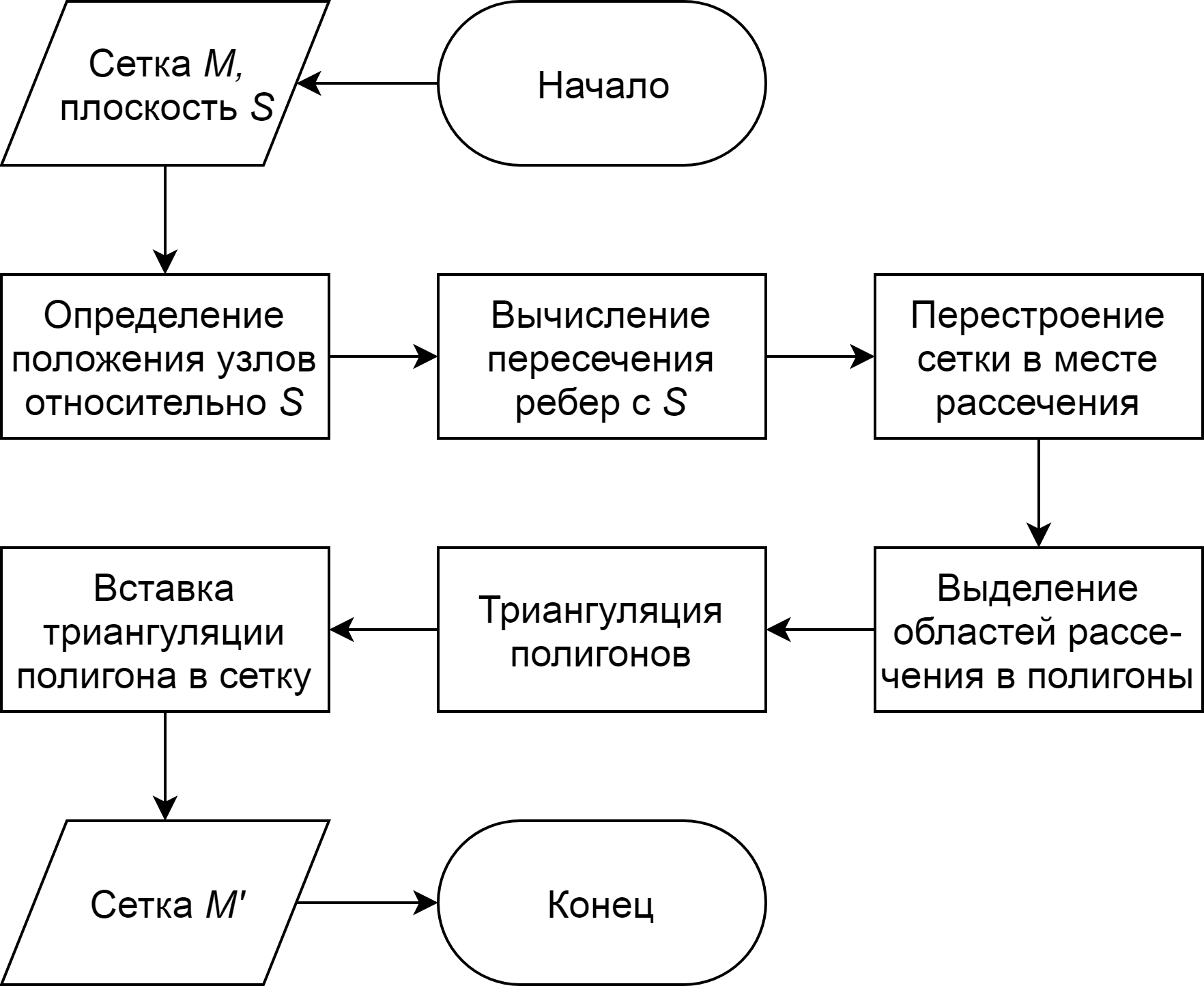
Далее мы рассмотрим каждый этап подробнее. Но для начала вспомним как вычислить точку пересечения отрезка и плоскости в пространстве.
Точка пересечения отрезка и плоскости
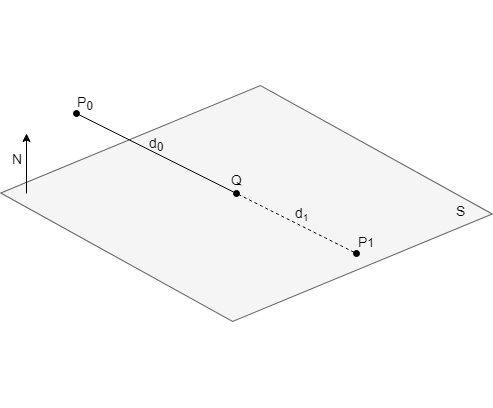
Точка пересечения отрезка, образованного точками P0 и P1, и плоскости S с нормалью N вычисляется по следующей формуле (1) из [2, с2]:
$$Q=P_0 + ( d_0 / (d_0-d_1) ) ( P_1 - P_0 )$$
где - d0 расстояние от точки P0 до плоскости S, d1 - расстояние от точки P1 до плоскости S.
Расстояние d от точки до плоскости вычисляем по следующей формуле (2), где Ps - это некоторая точка на плоскости S:
$$d=N_x ( P_x - P_{sx} ) + N_y ( P_y - P_{sy} ) + N_z ( P_z - P_{sz} )$$
Если d>0, то точка P находится с лицевой стороны плоскости S. Если d<0, то точка P находится с тыльной стороны плоскости S. Если d=0, то точка P лежит на плоскости S.
Определение относительного положения узлов сетки
На начальном этапе алгоритма разбиения промаркируем узлы сетки M в соответствии с их положением относительно секущей плоскости S. Узлы могут оказаться с лицевой стороны плоскости, с ее тыльной стороны или лежать на плоскости. Лицевая сторона плоскости определяется по направлению ее нормали N.
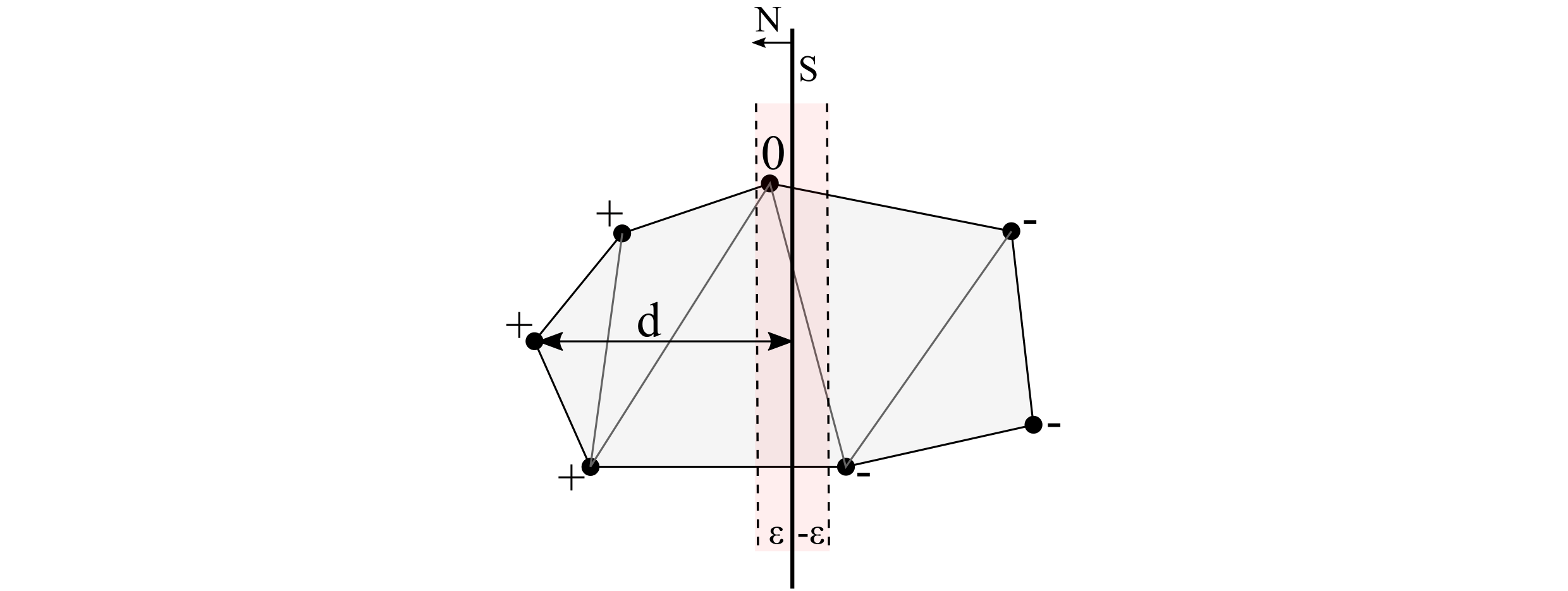
Для каждого узла вычисляется его расстояние d до плоскости (формула 2 выше) и выбирается одно из трех положений: лицевая область (рисунок ниже, узлы со знаком "+"), тыльная область (узлы со знаком "-") или положение на секущей плоскости (узлы со знаком "0"). Так как для обозначения координат узлов используются вещественные числа, равенство следует проверять с учетом некоторой погрешности ε. Тогда для узлов, лежащих на плоскости, справедливо неравенство:
$$-\varepsilon <= d <= +\varepsilon$$
Если в конечном итоге оказывается, что сетка M не имеет узлов с тыльной или лицевой стороны плоскости, то мы делаем вывод, что плоскость S не пересекает сетку M.
Пересечение ребер плоскостью
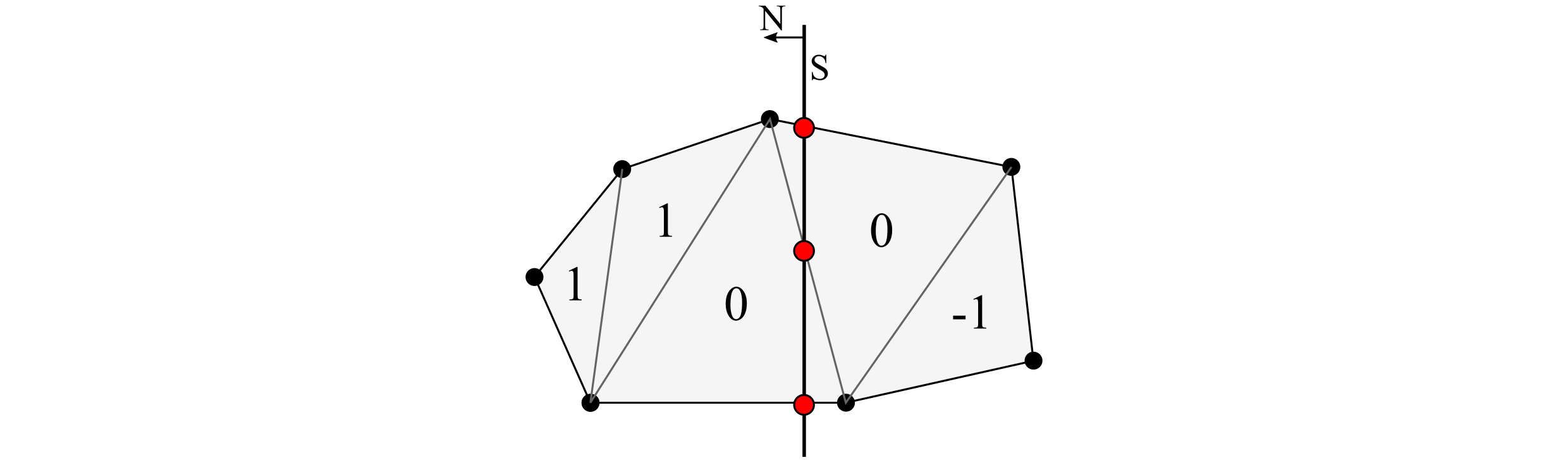
На следующем этапе алгоритма выполняем обход по всем треугольникам сетки (или ребрам, или узлам — зависит от выбранной структуры данных) и вычисляем точки пересечения их ребер с секущей плоскостью. При этом каждый треугольник получает один из следующих маркеров:
"1" — треугольник находится с лицевой стороны плоскости;
"0" — треугольник пересекается плоскостью;
"-1" — треугольник находится с тыльной стороны плоскости.
Перестроение сетки в месте пересечения
После того, как треугольники промаркированы, начинается сборка результирующей сетки M' с перестроением треугольников в местах пересечения, то есть треугольников с маркером "0". Результирующей может быть сетка как с лицевой стороны секущей плоскости, так и с тыльной. В зависимости от требуемого результата, соответствующие треугольники с маркерами "1" или "-1" будут добавляться в новую сетку без изменений.
Для рассеченных треугольников необходимо выполнить перестроения геометрии. На рисунке ниже показаны частные случаи перестроения треугольников, где e, e1 и e2 - добавляемые ребра с новыми узлами в местах пересечения.
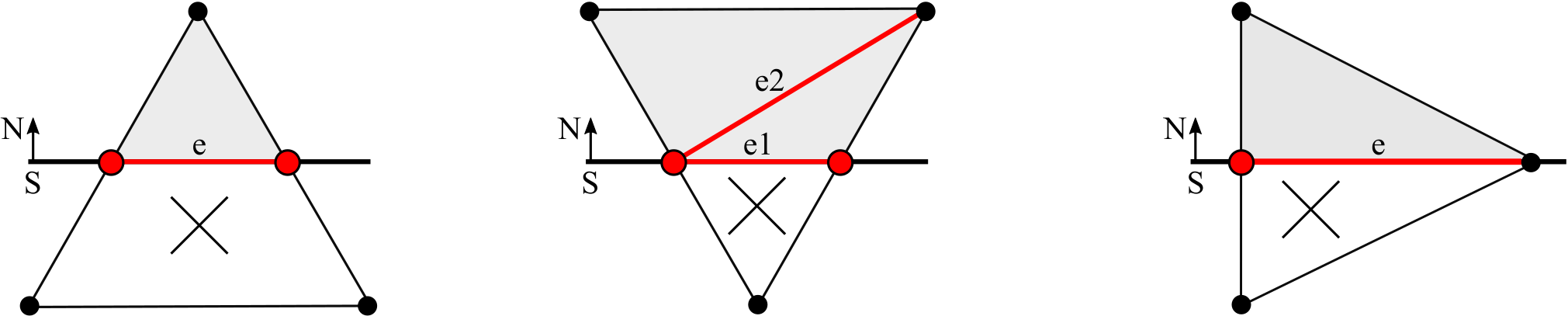
После выполнения этого шага мы получаем отсеченную часть исходной сетки с пустотой в месте рассечения.
Выделение двумерных полигонов в месте рассечения
Пустоту, образовавшуюся в области рассечения, требуется заполнить триангуляцией. Так как все узлы и ребра в месте рассечения лежат в одной плоскости, упростим задачу и представим такую область в виде двумерного полигона. Полигон состоит из одного внешнего и множества внутренних контуров, имеющих определенный порядок обхода узлов.
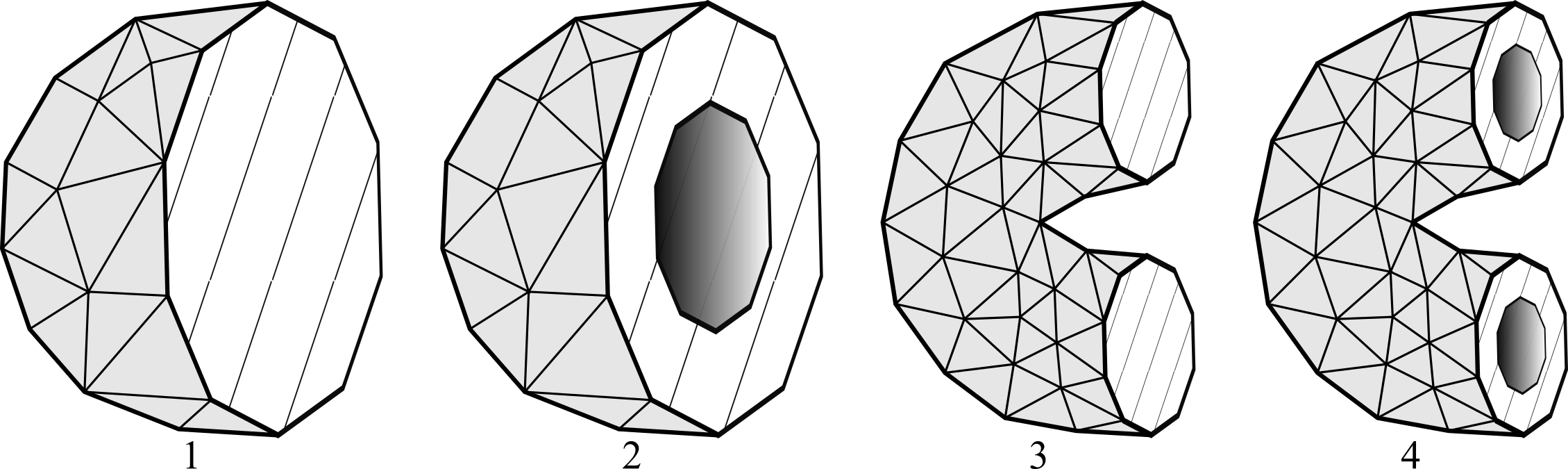
Выделим четыре основных варианта полигонов в области рассечения сетки:
Один полигон без внутренних контуров;
Один полигон с одним или несколькими внутренними контурами;
Несколько полигонов без внутренних контуров;
Несколько полигонов, содержащих внутренние контуры.
Определим алгоритм выделения таких двумерных полигонов из рассеченной сетки, полученной на предыдущем этапе. Он включает в себя два основных этапа:
Поиск всех контуров в месте рассечения;
Компоновка полигонов из полученных контуров.
Каждый треугольник, граничащий с местом рассечения, отличается от остальных тем, что он не имеет с одной из своих сторон соседа. Узлы и ребра, находящиеся на границе рассечения, как раз и формируют будущий контур.
Собирать контуры будем путем движения фронта по треугольникам вдоль границы рассечения, пока он не будет замкнут на начальном треугольнике (см. схему ниже). Каждый пройденный треугольник помечаем. Последовательность шагов выглядит следующим образом:
Поиск первого граничного треугольника T0;
Добавление граничных узлов треугольника <ni, nj>, которые еще не были добавлены в контур;
Пометка текущего треугольника;
Переход к соседнему граничному треугольнику Ti. Если следующий треугольник найден и он не T0, то идем в п.2, иначе завершаем построение контура.
После построения контура необходимо обойти оставшиеся треугольники сетки и проверить их на наличие граничных ребер. Если граничный треугольник будет найден, то повторить процедуру для построения следующего контура.
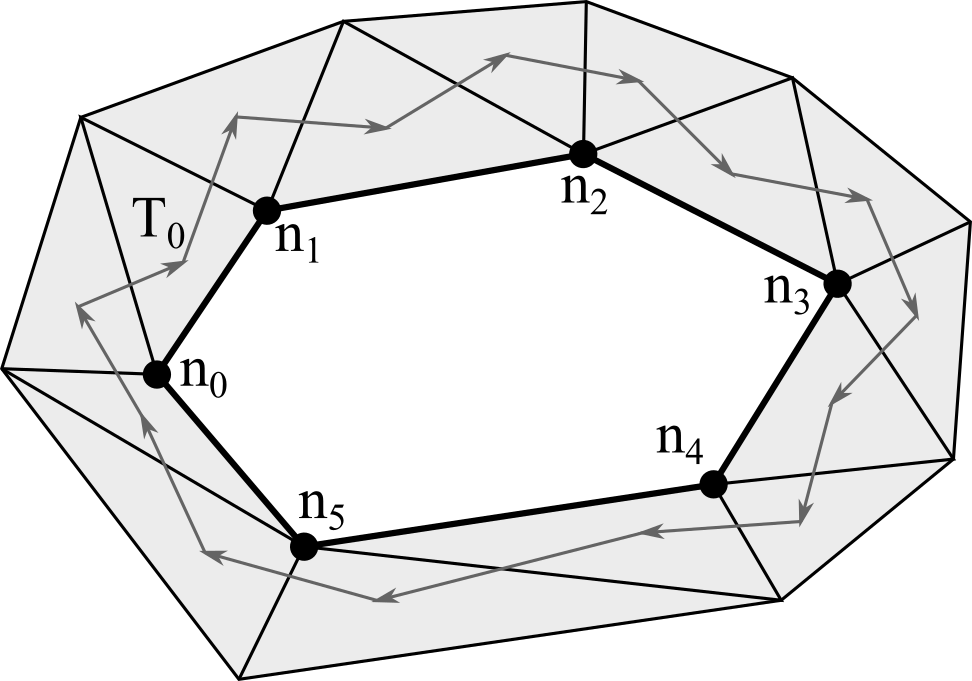
При добавлении в контур первого узла n0 нужно запомнить вектор D0 нормали треугольника (рисунок ниже). Этот вектор поможет определить ориентацию контура в будущем полигоне: внутренний или внешний.
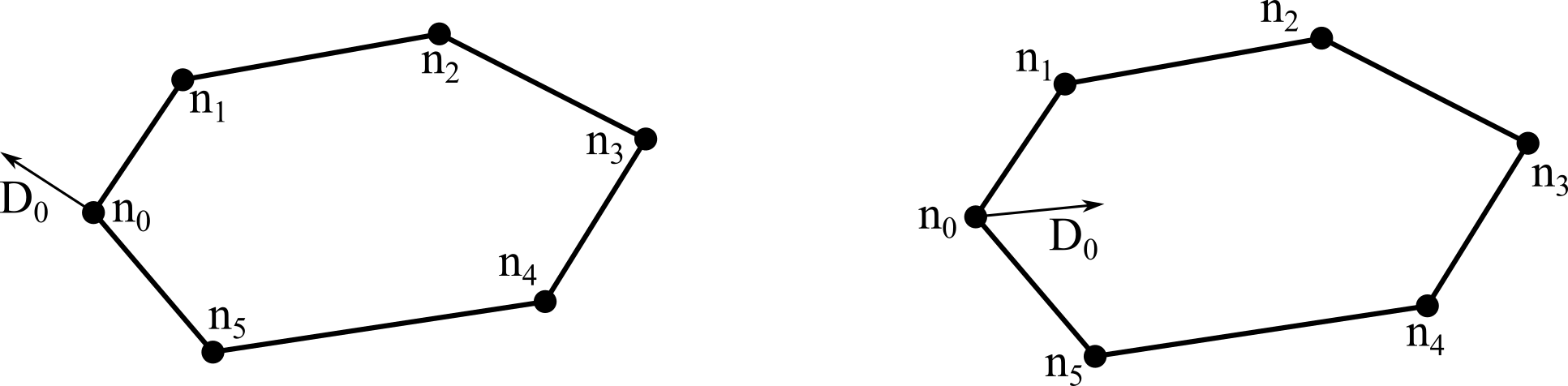
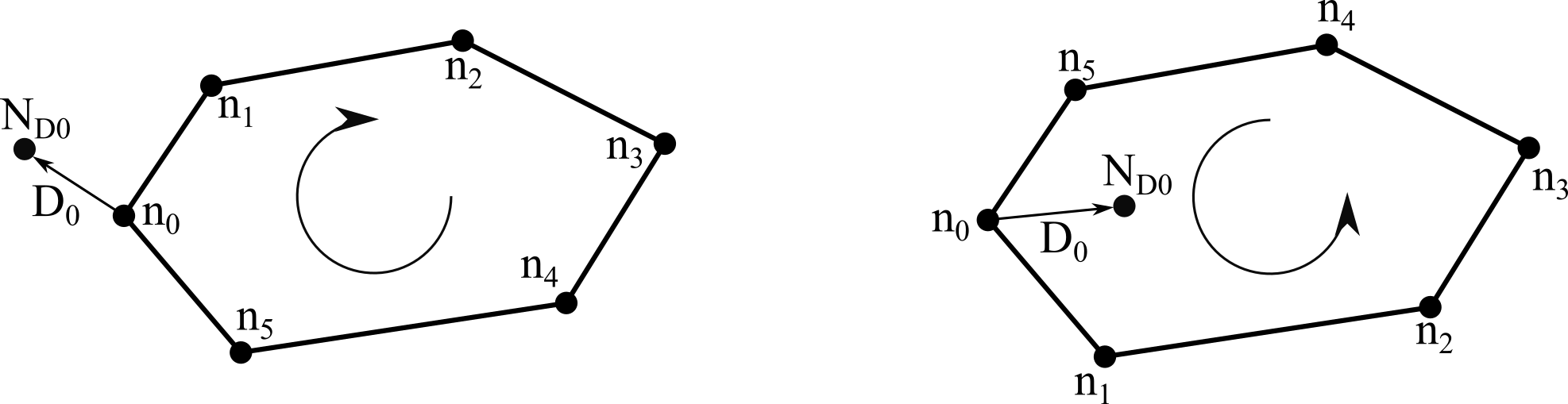
Пусть точка ND0 - это некоторая точка на векторе D0 (рисунок ниже). Если рассматриваемый контур - внешний, то при обходе контура по часовой стрелке точка ND0 будет находится слева от него, а при обходе контура против часовой — справа. Все остальные контуры автоматически обозначаем как внутренние, так как внешний контур у полигона может быть только один.
Определить направление обхода контура можно по его трем последовательным точкам [3, с 95]. При этом в качестве средней из трех точек на контуре лучше выбрать самую правую по координате x, а если таких несколько, то самую верхнюю из них (с наибольшей координатой y). Положение точки ND0 (слева или справа) можно определить относительно ребра (n0, n1) [3, с 96].
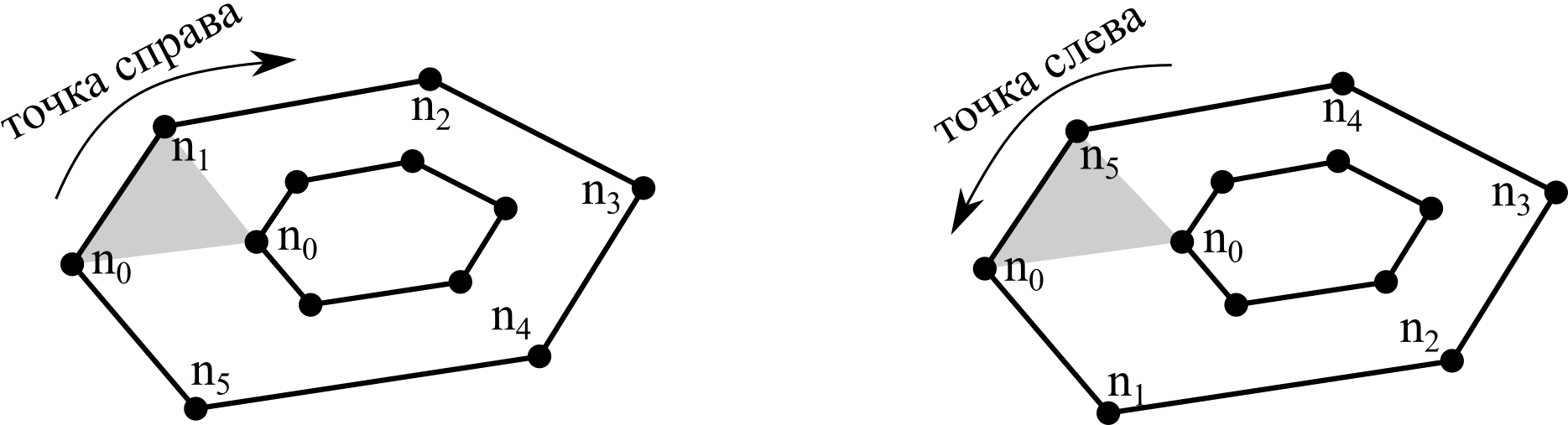
Наконец, сформируем из полученного множества контуров полигоны. Каждый внешний контур определяет один полигон. Для внутренних контуров требуется понять в какой из внешних они попадают и соответственно связать их в одну структуру данных. Так как все контуры множества не пересекаются, то для определения принадлежности внутреннего контура достаточно проверить положение любой его точки относительно всех ребер рассматриваемого внешнего контура (рисунок ниже). При обходе внешнего контура по часовой стрелке внутренняя точка всегда находится справа, при обходе против часовой — слева.
Триангуляция двумерных полигонов
Существуют разные способы создания триангуляции для множества точек на плоскости. Наша задача заключается в создании триангуляции полигона, который может включать внутренние контуры. Наиболее простым и в то же время достаточно эффективным является семейство итеративных алгоритмов триангуляции. Об этих алгоритмах подробно рассказано в работе [1].
В общем случае триангуляция полигона итеративным алгоритмом включает следующие этапы:
Построение триангуляции по всем точкам полигона без учета его ребер.
Вставка в триангуляцию всех ребер полигона, называемых структурными отрезками.
Удаление из триангуляции треугольников, находящихся за пределами полигона.
Рассмотрим простой итеративный алгоритм триангуляции с ограничениями. Ограничениями в триангуляции называются структурные ребра полигона.
Шаг 1. Построение суперструктуры [1, c 32]. Суперструктура охватывает все точки данного полигона (рисунок ниже, слева). Поэтому каждая новая точка, добавляемая в триангуляцию, всегда будет попадать на какой-либо из существующих треугольников. В качестве суперструктуры используем прямоугольник. Его легко построить и определить начальную триангуляцию в виде двух треугольников (рисунок 13, справа).
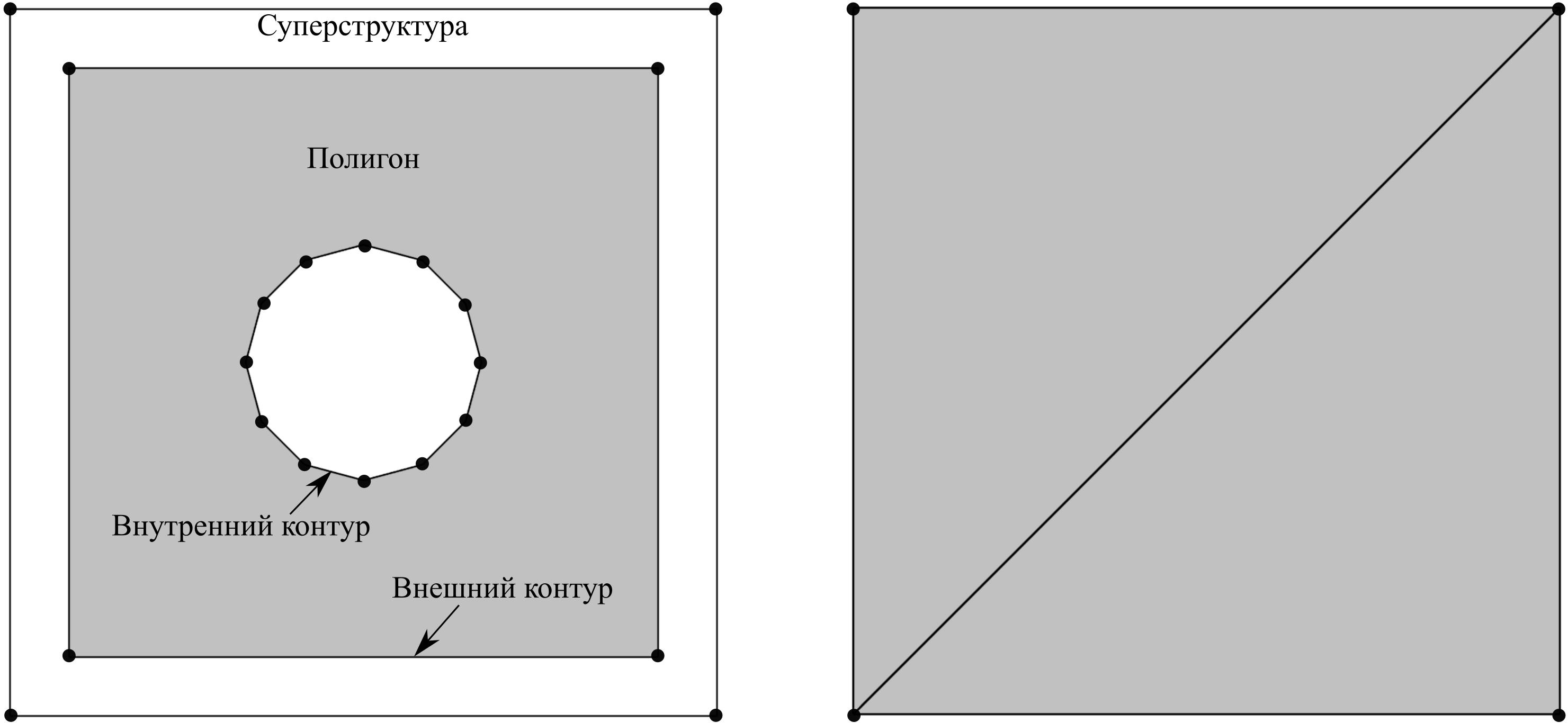
Шаг 2. Вставка всех точек полигона в триангуляцию [1, c 31]. Для каждой точки полигона находим треугольник, в который она попадает [1, c 33], и разбиваем его на три новых треугольника. В результате получаем триангуляцию полигона без учета структурных отрезков. Поиск треугольника, в который попадает точка, может быть реализовано по-разному. Самым простым в реализации мне показался способ 3 в [1, c 34].
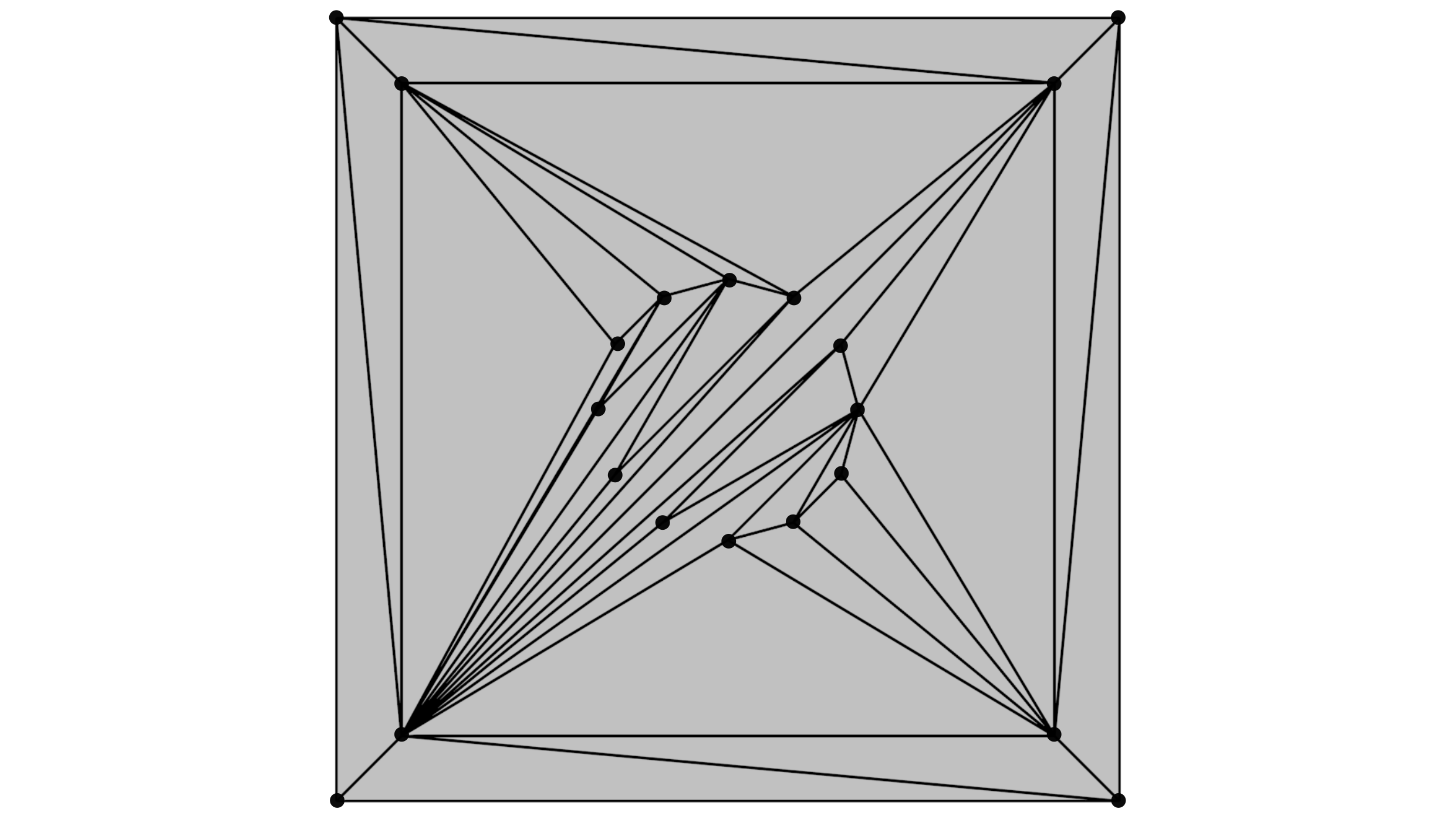
Шаг 3. Вставка всех структурных ребер полигона (рисунок ниже). Выберем способ вставки «Удаляй и строй» [1, c 74]. При вставке ребра сначала удаляются все треугольники, которые оно пересекает, а затем образовавшийся в месте удаления ребер многоугольник разбивается вставляемым ребром на два и полученные многоугольники заполняется триангуляцией. Неплохой способ заполнения триангуляцией левой и правой частей многоугольника указан в этом же разделе [1, c 74].
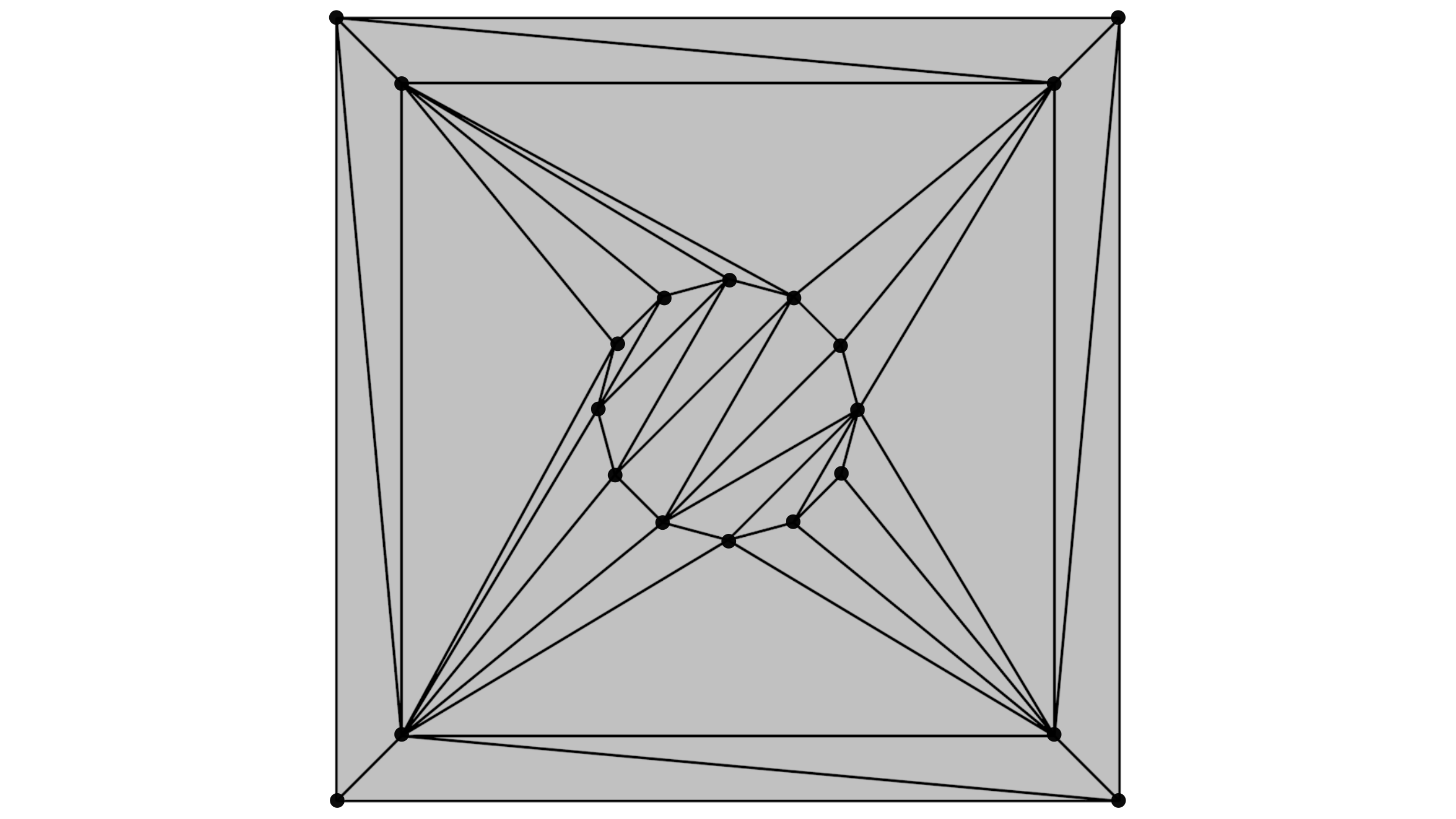
Шаг 4. Удаление треугольников, выходящих за пределы полигона. На данном этапе решается задача классификации треугольников по признаку попадания внутрь области полигона ([1, c 78] или [4, с 4]). Делая обход триангуляции, начиная с любого треугольника, лежащего внутри полигона, (рисунок ниже, слева) помечаем все треугольники, не выходя за пределы, ограниченные структурными отрезками. Остальные треугольники отбрасываются из структуры (рисунок ниже, справа). Начальный треугольник можно определить по структурному ребру внешнего контура. Так как ребро содержит информацию о примыкающих треугольниках и нам известно направление обхода контура, то можно определить с какой стороны от ребра находятся каждый из двух треугольников.
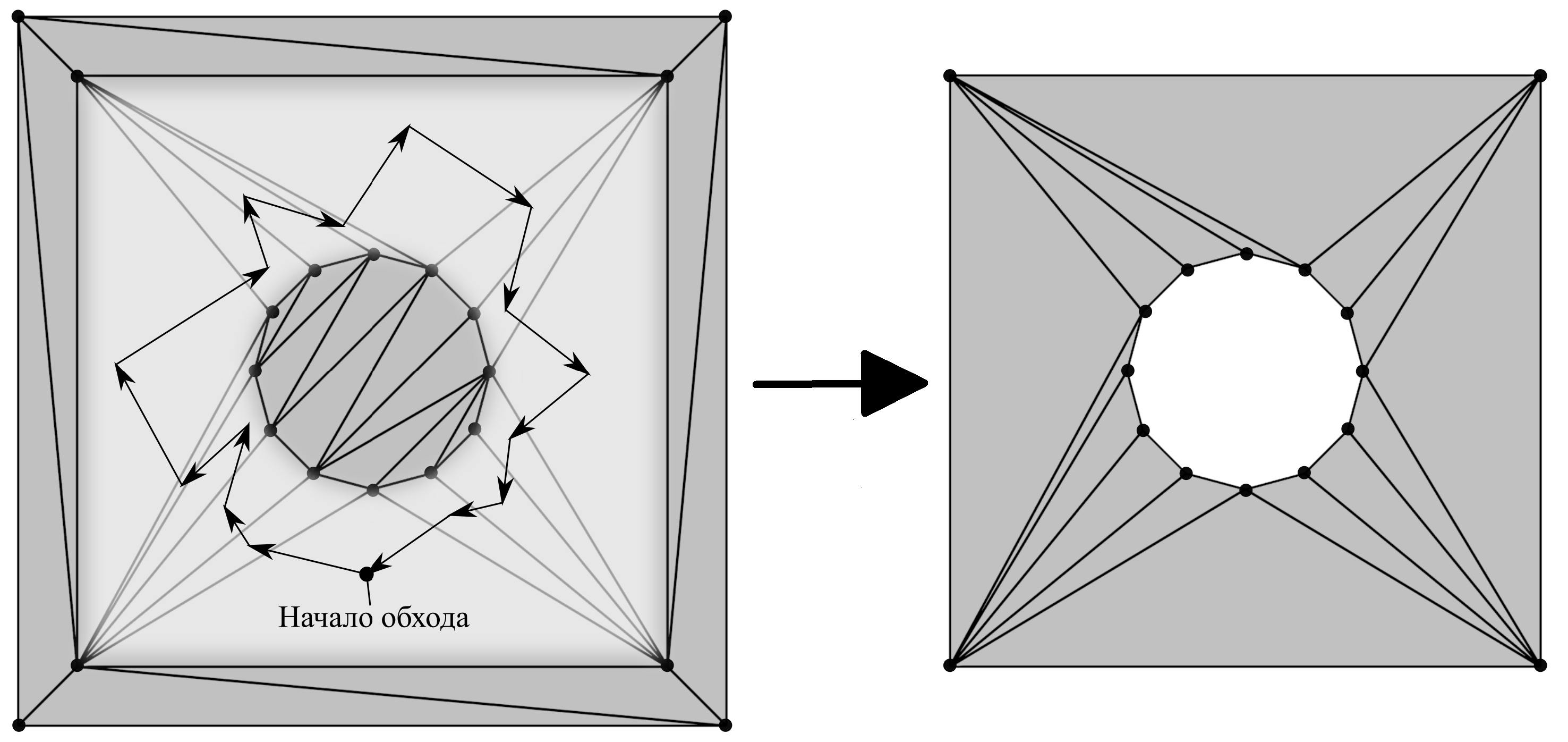
Вставка триангуляции полигона в трехмерную сетку
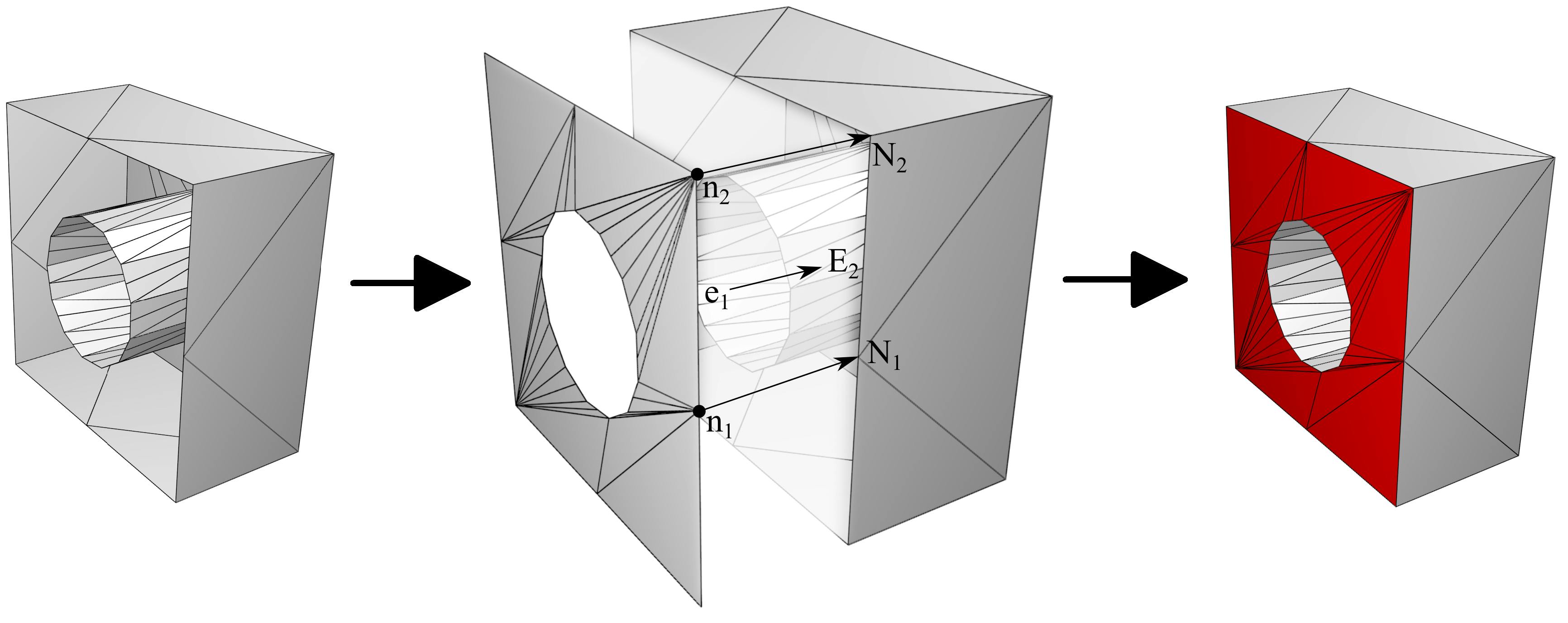
При вставке триангуляции полигона в итоговую сетку M' будут добавлены новые ребра и треугольники. Сетка станет пространственно замкнутой. Новые узлы при этом не добавляются, так как триангуляция полигона строилась исключительно с использованием существующих узлов на границе среза. Наиболее простой на мой взгляд в реализации способ объединения двух триангуляций — с помощью таблиц ассоциаций индексов элементов (узлов и ребер). Тогда для каждого полигона мы имеем ассоциации «индекс узла сетки — индекс узла полигона» и «индекс ребра сетки — индекс ребра полигона». Двигаясь по треугольникам полигона, мы можем точно знать в какое место его следует поместить в итоговой сетке. На рисунке 17 показаны ассоциации <ei, Ej> для ребер и <ni, Nj> для узлов, где i - индексы элементов полигона, j - индексы элементов сетки.
Заключение
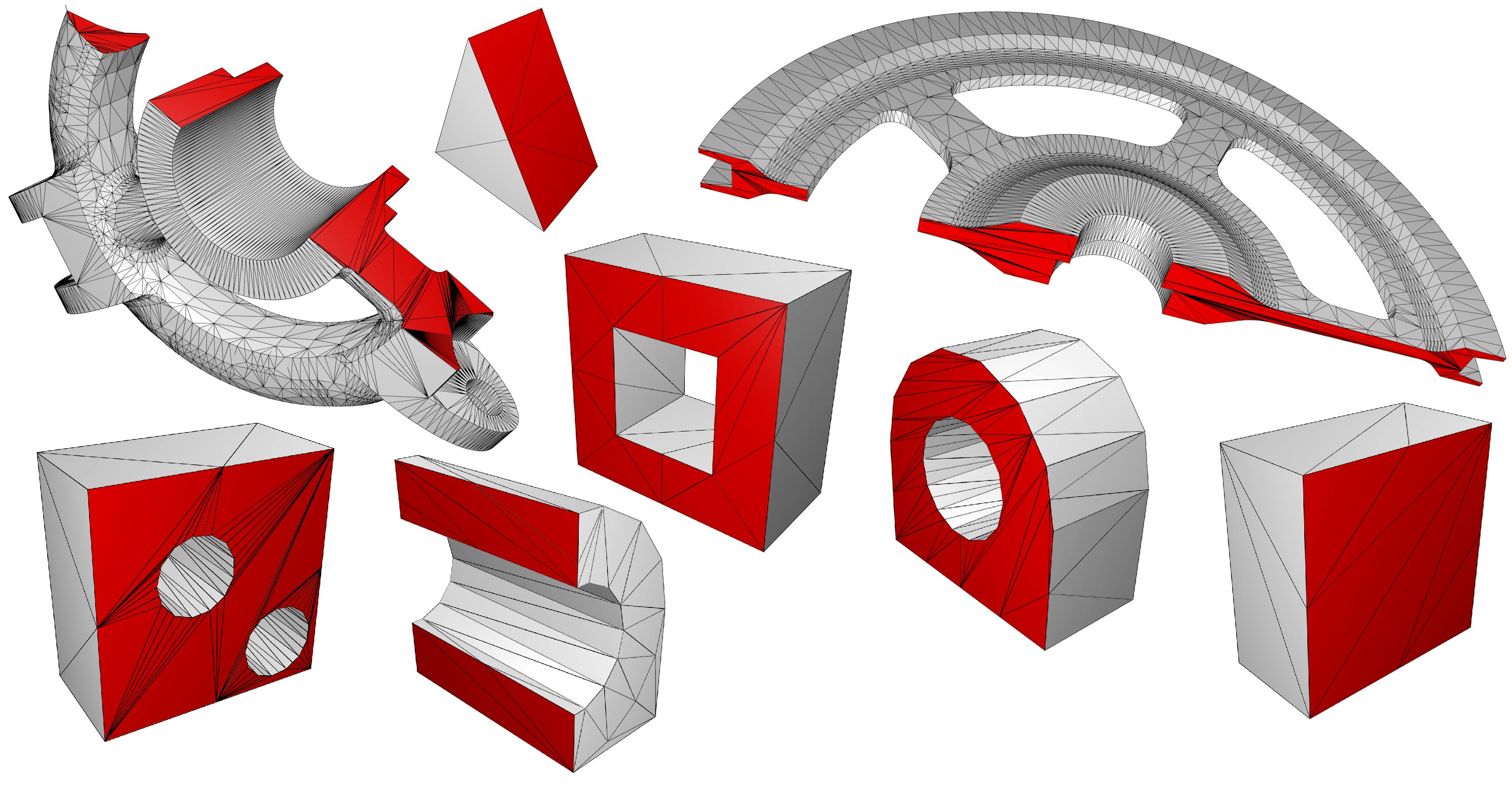
На рисунке ниже показаны несколько примеров разбиений триангуляционных сеток описанным алгоритмом. Стоит сказать, что алгоритм может строить вытянутые, или "игольчатые", треугольники. Однако в нашем случае это не имеет значения, так как на данный момент сетка используется только для визуализации и никаких дальнейших вычислительных операций над ней не производится. При необходимости можно выполнить перестроения [1].